Advanced of the Machine Learning Toolkit

This work represents a deep dive into the practical application of machine learning algorithms. Across several projects, key algorithms were evaluated using industry-standard tools like Scikit-learn for core models, Matplotlib for visualization, and Gymnasium (Gym) for reinforcement learning environments, alongside custom implementations for randomized optimization. The primary goal was to understand algorithm performance, applicability, and the nuances of hyperparameter tuning across diverse problems.

Here’s a glimpse:

Predicting Outcomes (Supervised Learning with Scikit-learn)

• Addressed prediction tasks using datasets like the noisy Titanic survival records and the structured Date Fruit classifications.
• Compared standard Scikit-learn implementations: Decision Trees, Neural Networks (NN), Support Vector Machines (SVM), K-Nearest Neighbors (KNN), and AdaBoost (Boosting). Fine-tuning involved techniques like cost-complexity pruning (ccp_alpha) for Decision Trees and optimizing network architecture/solvers for Neural Networks.

  • Example: Analyzing Decision Tree pruning by comparing the number of nodes pruned versus ccp_alpha for Gini and Entropy criteria on the Titanic dataset. Gini proved more stringent and effective here.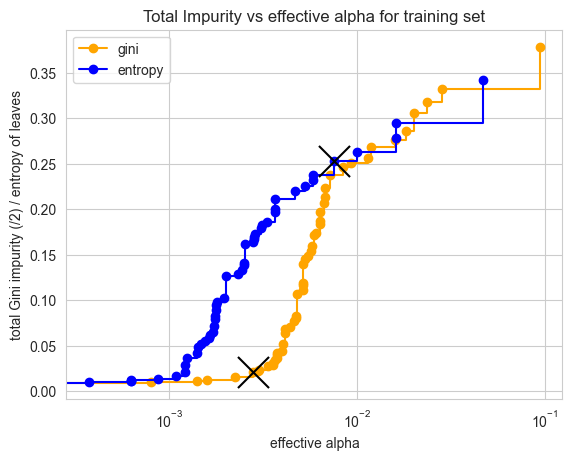

    

  • Example: Visualizing learning curves helps diagnose bias and variance, guiding model selection and hyperparameter tuning.

    

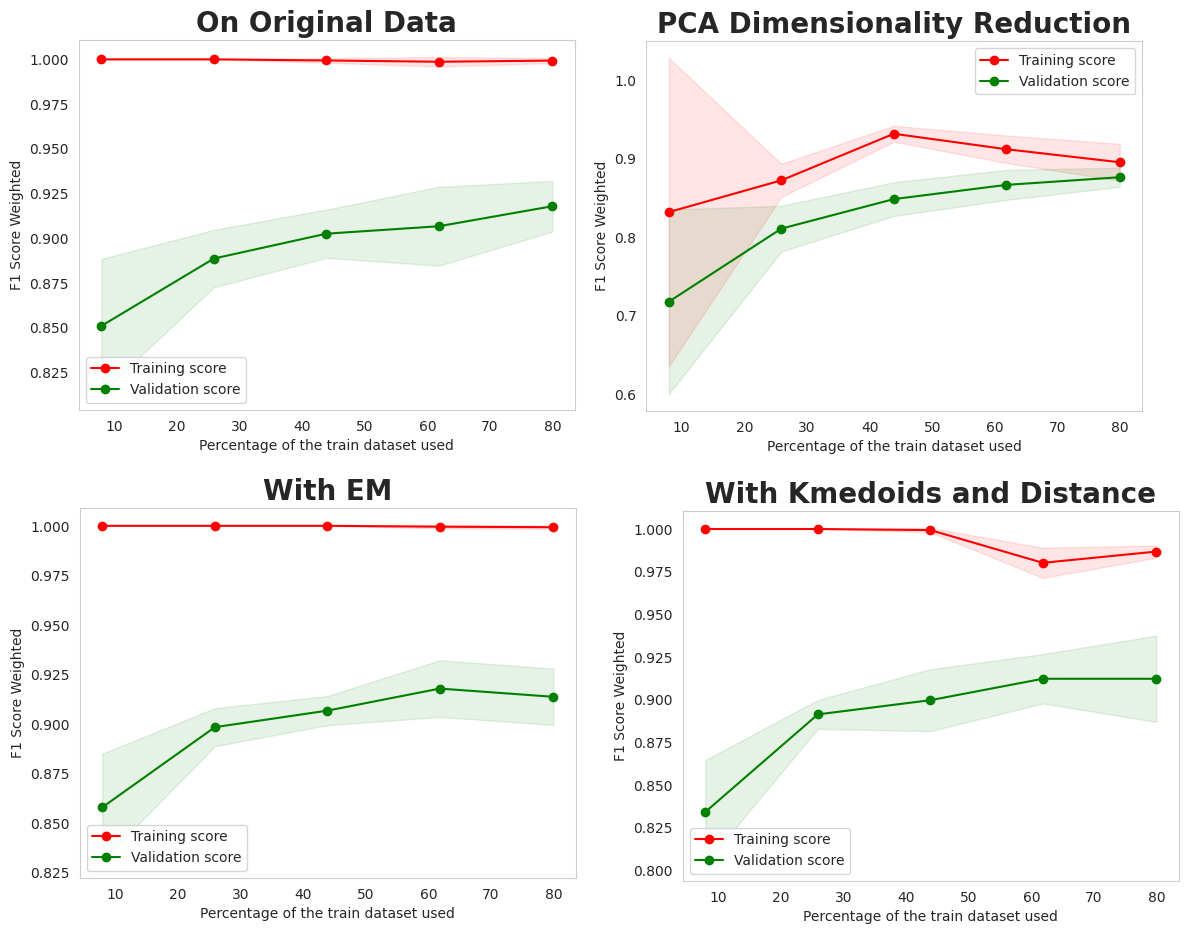
• Key Insight: Performance is highly context-dependent. SVM excelled on the clean, structured Date Fruit data (F1: 0.933), while KNN was surprisingly effective on the preprocessed, noisier Titanic data (F1: 0.822). Success hinges on matching the algorithm and its tuning to the data’s characteristics.

Finding the Best Solutions (Randomized Optimization - Custom Library)

• Implemented and compared Randomized Hill Climbing (RHC), Genetic Algorithms (GA), Simulated Annealing (SA), and MIMIC using a custom optimization library.
• Applied these algorithms to classic optimization problems: Traveling Salesman Problem (TSP), N-Queens, and FlipFlop. Tuning involved parameters like population size, mutation rate (GA), keep percentage (MIMIC), and temperature/decay schedules (SA).

  • Example: GA tuning for TSP involved balancing population size and mutation rate for effective exploration versus exploitation.

    

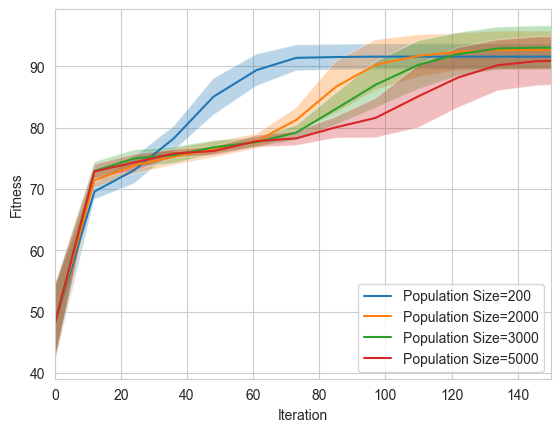
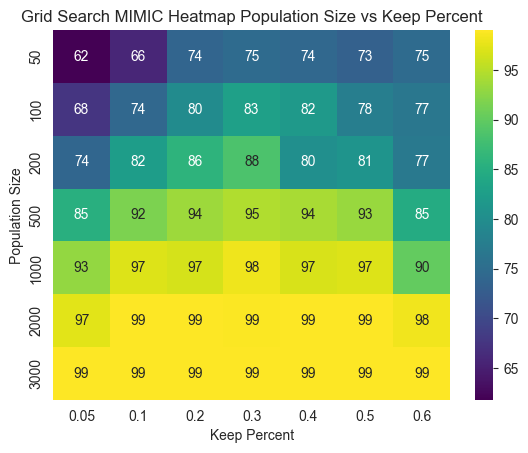
  • Example: MIMIC’s performance on the FlipFlop problem highlighted its strength in modeling structured problems, achieving optimal solutions efficiently by tuning population size and keep percentage.

    

• Key Result: Demonstrated Simulated Annealing could effectively optimize Neural Network weights for the Titanic dataset, achieving performance (F1: 0.78) comparable to traditional gradient descent (F1: 0.76) for the tested configuration, albeit with longer training times. GA struggled with this task.

Uncovering Patterns & Simplifying Data (Unsupervised Learning with Scikit-learn)

• Utilized Scikit-learn’s K-Medoids and Expectation-Maximization (EM with Gaussian Mixture Models) algorithms to discover clusters in both Titanic and Date Fruit datasets. K-Medoids showed better robustness on the noisy Titanic data (ARI: 0.11 vs 0.05 for EM). EM performed well on the Fruits data (ARI: 0.52).
• Leveraged dimensionality reduction techniques: Principal Component Analysis (PCA), Independent Component Analysis (ICA), Randomized Projections (RP), and Uniform Manifold Approximation and Projection (UMAP) to simplify data, enable visualization with Matplotlib, and potentially improve downstream tasks.

  • Example: ICA applied to the Fruits dataset revealed components aggregating related original features (e.g., color attributes), visualized via the mixing matrix.

    

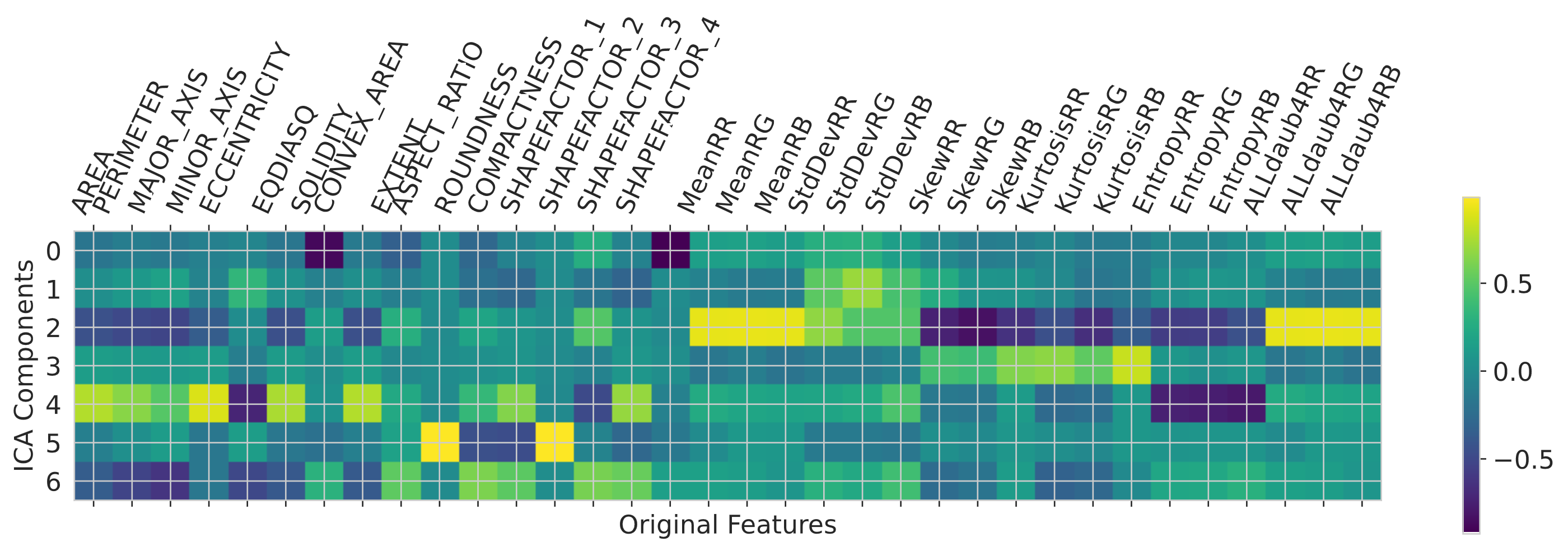
• Highlight: Dimensionality reduction, particularly UMAP, proved effective at simplifying high-dimensional data (like Fruits) while preserving structure, leading to improved performance for simple classifiers like Decision Trees in the reduced space. PCA also showed benefits for creating lightweight NN models on the Fruits data.

Teaching Agents to Decide (Reinforcement Learning with Gymnasium)

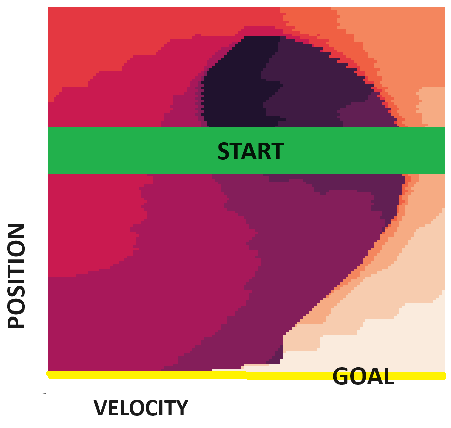
• Developed agents to learn optimal policies in Gymnasium (Gym) environments: the stochastic, discrete Frozen Lake and the continuous-control Mountain Car (discretized).

  • Example: Understanding the Mountain Car environment dynamics (position, velocity) is crucial for devising strategies to reach the goal.

    

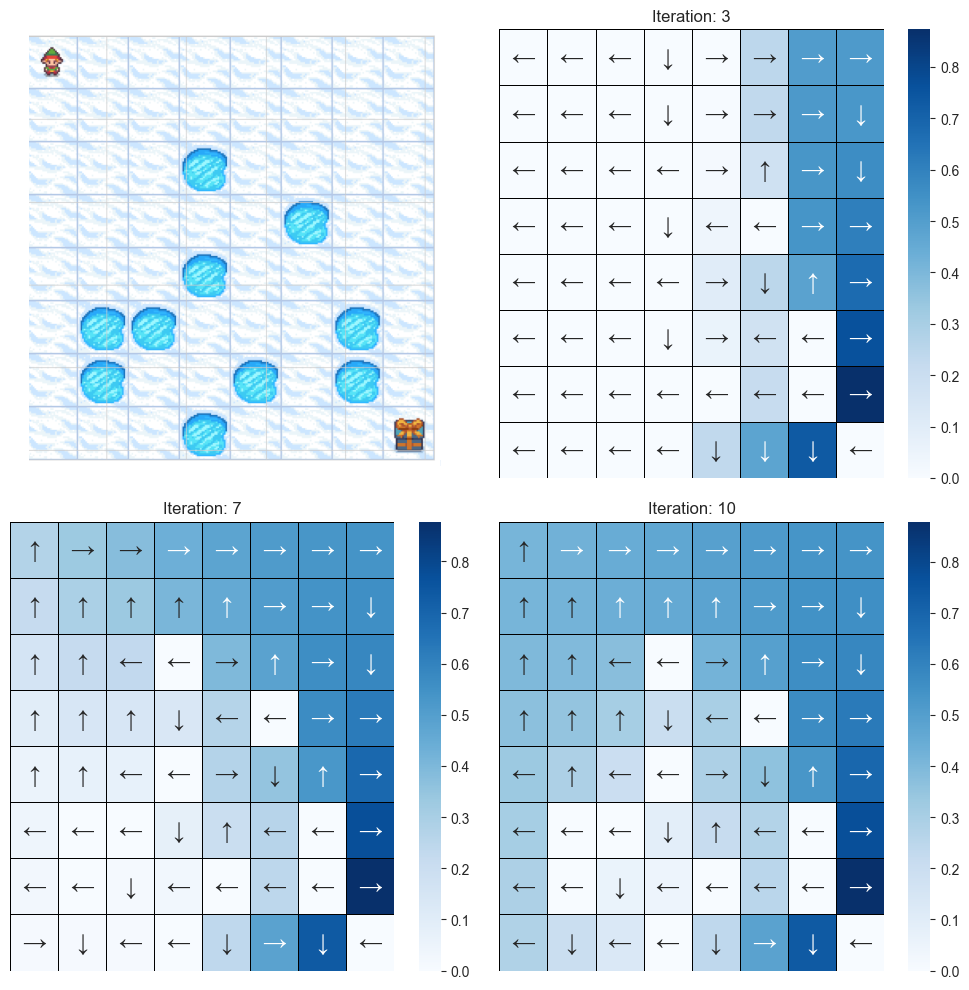
• Implemented and compared model-based (Value Iteration, Policy Iteration) and model-free (Q-Learning) RL methods. Analyzed the impact of hyperparameters like the discount factor (γ) and learning rate (α).

  • Example: Comparing the optimal policies found by Value Iteration and Policy Iteration on Frozen Lake often shows convergence to similar solutions, though PI can be faster for smaller state spaces.

    

  • Example: Analyzing Policy Iteration performance on Mountain Car with varying discount factors (γ) demonstrates how prioritizing long-term rewards affects the learned policy.

    

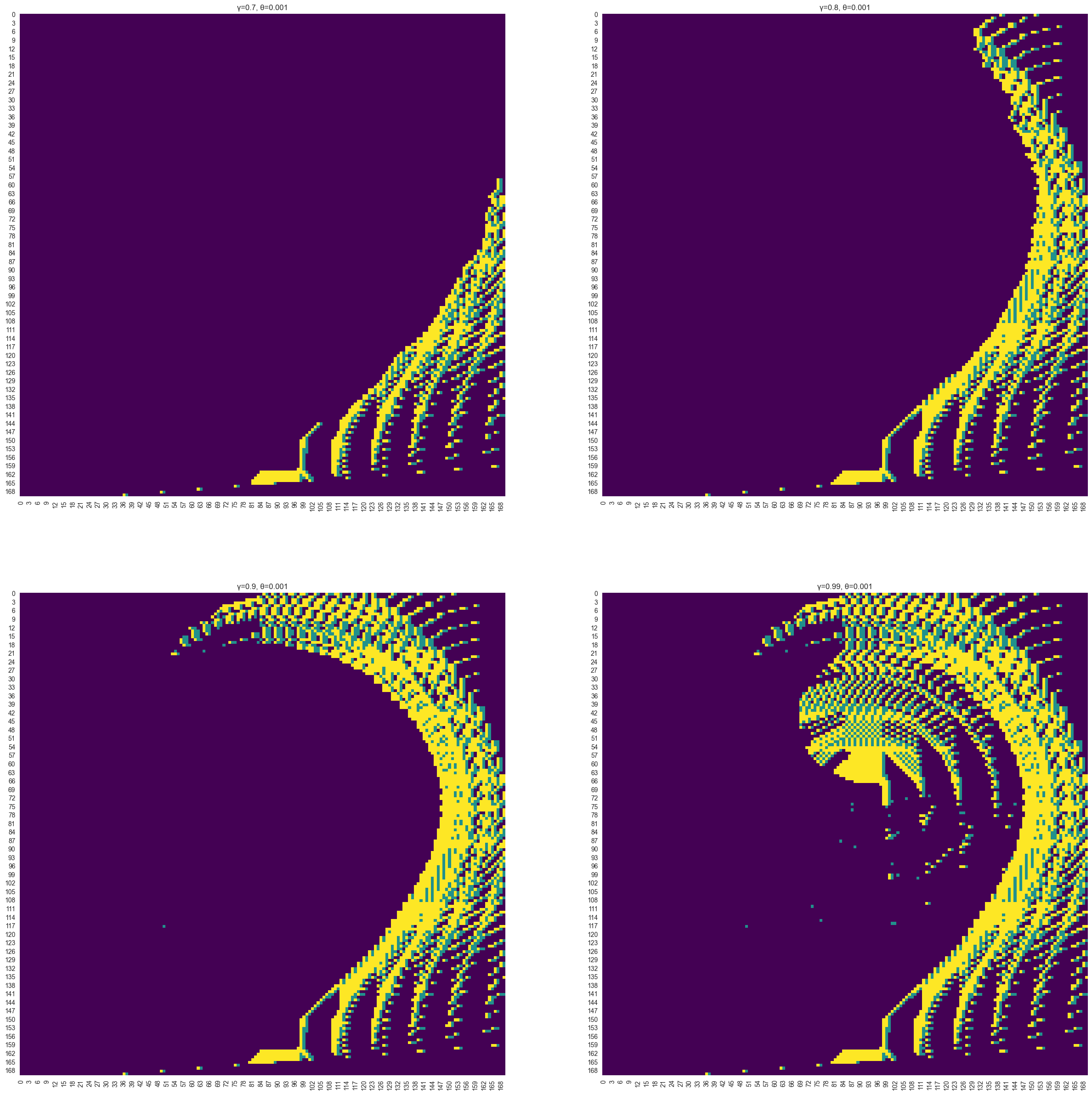
• Learning: Showcased how environment characteristics (stochasticity, reward sparsity) and hyperparameter tuning (e.g., γ, ε-decay in Q-learning) drastically influence algorithm effectiveness and convergence. Q-learning, while slower on Frozen Lake, outperformed VI/PI on the discretized Mountain Car due to challenges in modeling transitions accurately for VI/PI with the chosen discretization.

Overall: This work demonstrates hands-on experience across the ML spectrum using key libraries (Scikit-learn, Matplotlib, Gymnasium) and custom implementations. It showcases the ability to select, implement, tune, and critically evaluate algorithms for diverse tasks like prediction, optimization, clustering, dimensionality reduction, and sequential decision-making, emphasizing the importance of matching techniques to problem specifics.

Key Technologies:

• Core Libraries: Python, NumPy, Pandas, Matplotlib, Scikit-learn, Gymnasium (Gym)
• Randomized Optimization: Randomized Hill Climbing (RHC), Genetic Algorithms (GA), Simulated Annealing (SA), MIMIC
• Supervised Learning: Decision Trees, Neural Networks (NN), Support Vector Machines (SVM), K-Nearest Neighbors (KNN), AdaBoost (Boosting)
• Unsupervised Learning: K-Medoids, Expectation-Maximization (EM), Principal Component Analysis (PCA), Independent Component Analysis (ICA), Randomized Projections (RP), Uniform Manifold Approximation and Projection (UMAP)
• Reinforcement Learning: Value Iteration, Policy Iteration, Q-Learning